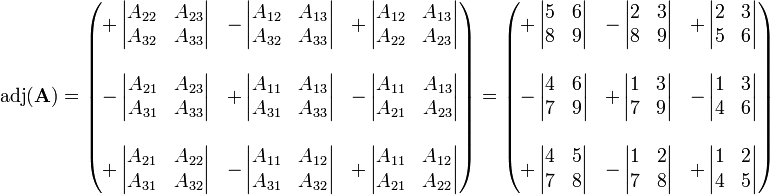adjoint matrix, minor, cofactor

336x280(권장), 300x250(권장), 250x250, 200x200 크기의 광고 코드만 넣을 수 있습니다.

소행렬식 = minor

여인자 = cofactor

의 n차의 정사각행렬 A=[a_ij]의 성분 a_ij의 여인자를 A_ij라 할 때, 행렬 [A_ij]^T를 A의 수반행렬(adjoint matrix)이라 하고, adj A 로 나타낸다. 즉,

ex2> http://en.wikipedia.org/wiki/Adjugate

2 × 2 generic matrix

The adjugate of the 2 × 2 matrix

$\mathbf{A} = \begin{pmatrix} {{a}} & {{b}}\\ {{c}} & {{d}} \end{pmatrix}$

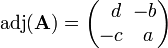$\operatorname{adj}(\mathbf{A}) = \begin{pmatrix} \,\,\,{{d}} & \!\!{{-b}}\\ {{-c}} & {{a}} \end{pmatrix}$ .

[edit] 3 × 3 generic matrix

Consider the $3\times 3$ matrix

$\mathbf{A} = \begin{pmatrix} A_{11} & A_{12} & A_{13} \\ A_{21} & A_{22} & A_{23} \\ A_{31} & A_{32} & A_{33} \end{pmatrix} = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}$ .

Its adjugate is the transpose of the cofactor matrix

$\mathbf{C} = \begin{pmatrix} +\left| \begin{matrix} A_{22} & A_{23} \\ A_{32} & A_{33} \end{matrix} \right| & -\left| \begin{matrix} A_{21} & A_{23} \\ A_{31} & A_{33} \end{matrix} \right| & +\left| \begin{matrix} A_{21} & A_{22} \\ A_{31} & A_{32} \end{matrix} \right| \\ & & \\ -\left| \begin{matrix} A_{12} & A_{13} \\ A_{32} & A_{33} \end{matrix} \right| & +\left| \begin{matrix} A_{11} & A_{13} \\ A_{31} & A_{33} \end{matrix} \right| & -\left| \begin{matrix} A_{11} & A_{12} \\ A_{31} & A_{32} \end{matrix} \right| \\ & & \\ +\left| \begin{matrix} A_{12} & A_{13} \\ A_{22} & A_{23} \end{matrix} \right| & -\left| \begin{matrix} A_{11} & A_{13} \\ A_{21} & A_{23} \end{matrix} \right| & +\left| \begin{matrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{matrix} \right| \end{pmatrix} = \begin{pmatrix} +\left| \begin{matrix} 5 & 6 \\ 8 & 9 \end{matrix} \right| & -\left| \begin{matrix} 4 & 6 \\ 7 & 9 \end{matrix} \right| & +\left| \begin{matrix} 4 & 5 \\ 7 & 8 \end{matrix} \right| \\ & & \\ -\left| \begin{matrix} 2 & 3 \\ 8 & 9 \end{matrix} \right| & +\left| \begin{matrix} 1 & 3 \\ 7 & 9 \end{matrix} \right| & -\left| \begin{matrix} 1 & 2 \\ 7 & 8 \end{matrix} \right| \\ & & \\ +\left| \begin{matrix} 2 & 3 \\ 5 & 6 \end{matrix} \right| & -\left| \begin{matrix} 1 & 3 \\ 4 & 6 \end{matrix} \right| & +\left| \begin{matrix} 1 & 2 \\ 4 & 5 \end{matrix} \right| \end{pmatrix}$

So that we have

$\operatorname{adj}(\mathbf{A}) = \begin{pmatrix} +\left| \begin{matrix} A_{22} & A_{23} \\ A_{32} & A_{33} \end{matrix} \right| & -\left| \begin{matrix} A_{12} & A_{13} \\ A_{32} & A_{33} \end{matrix} \right| & +\left| \begin{matrix} A_{12} & A_{13} \\ A_{22} & A_{23} \end{matrix} \right| \\ & & \\ -\left| \begin{matrix} A_{21} & A_{23} \\ A_{31} & A_{33} \end{matrix} \right| & +\left| \begin{matrix} A_{11} & A_{13} \\ A_{31} & A_{33} \end{matrix} \right| & -\left| \begin{matrix} A_{11} & A_{13} \\ A_{21} & A_{23} \end{matrix} \right| \\ & & \\ +\left| \begin{matrix} A_{21} & A_{22} \\ A_{31} & A_{32} \end{matrix} \right| & -\left| \begin{matrix} A_{11} & A_{12} \\ A_{31} & A_{32} \end{matrix} \right| & +\left| \begin{matrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{matrix} \right| \end{pmatrix} = \begin{pmatrix} +\left| \begin{matrix} 5 & 6 \\ 8 & 9 \end{matrix} \right| & -\left| \begin{matrix} 2 & 3 \\ 8 & 9 \end{matrix} \right| & +\left| \begin{matrix} 2 & 3 \\ 5 & 6 \end{matrix} \right| \\ & & \\ -\left| \begin{matrix} 4 & 6 \\ 7 & 9 \end{matrix} \right| & +\left| \begin{matrix} 1 & 3 \\ 7 & 9 \end{matrix} \right| & -\left| \begin{matrix} 1 & 3 \\ 4 & 6 \end{matrix} \right| \\ & & \\ +\left| \begin{matrix} 4 & 5 \\ 7 & 8 \end{matrix} \right| & -\left| \begin{matrix} 1 & 2 \\ 7 & 8 \end{matrix} \right| & +\left| \begin{matrix} 1 & 2 \\ 4 & 5 \end{matrix} \right| \end{pmatrix}$

where

$\left| \begin{matrix} A_{im} & A_{in} \\ \,\,A_{jm} & A_{jn} \end{matrix} \right|= \det\left( \begin{matrix} A_{im} & A_{in} \\ \,\,A_{jm} & A_{jn} \end{matrix} \right)$ .

Note that the adjugate is the transpose of the cofactor matrix. Thus, for instance, the (3,2) entry of the adjugate is the (2,3) cofactor of A.

저작자표시 비영리 변경금지

'Mathematics > Linear Algebra' 카테고리의 다른 글

Matrix Algebra (0)	2011.12.21
Determinant (ex) det(A) , Sarrus, Laplace's formula and the adjugate matrix (0)	2011.12.21
homogemeous metrix, nonhomogemeous metrix (0)	2011.12.21

Professionality

adjoint matrix, minor, cofactor

[edit] 3 × 3 generic matrix

'Mathematics > Linear Algebra' 카테고리의 다른 글

티스토리툴바

adjoint matrix, minor, cofactor

[edit] 3 × 3 generic matrix

'Mathematics > Linear Algebra' 카테고리의 다른 글

'Mathematics/Linear Algebra' Related Articles

티스토리툴바