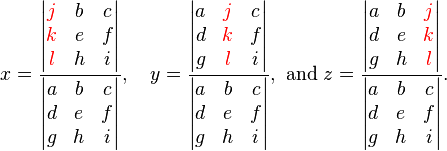http://en.wikipedia.org/wiki/Cramer's_rule
Consider a system of n linear equations for n unknowns, represented in matrix multiplication form as follows:
|
|
 |
where the n by n matrix A has a nonzero determinant, and the vector  is the column vector of the variables.
is the column vector of the variables.
Then the theorem states that in this case the system has a unique solution, whose individual values for the unknowns are given by:
where Ai is the matrix formed by replacing the ith column of A by the column vector b.
The rule holds for systems of equations with coefficients and unknowns in any field, not just in the real numbers. It has recently been shown that Cramer's rule can be implemented in O(n3) time,[3] which is comparable to more common methods of solving systems of linear equations, such as Gaussian elimination.
============================================================================================================
Explicit formulas for small systems
Consider the linear system 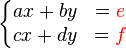 which in matrix format is
which in matrix format is  Then, x and y can be found with Cramer's rule as
Then, x and y can be found with Cramer's rule as
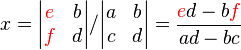 and
and
The rules for 3×3 are similar. Given 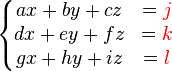 which in matrix format is
which in matrix format is
 the values of x, y and z can be found as follows:
the values of x, y and z can be found as follows:
'Mathematics > Linear Algebra' 카테고리의 다른 글
| Eigenvalues and eigenvectors, Characteristic polynomial (1) | 2011.12.26 |
|---|---|
| Matrix Algebra (0) | 2011.12.21 |
| adjoint matrix, minor, cofactor (2) | 2011.12.21 |

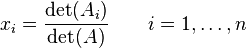
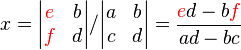 and
and
 the values of x, y and z can be found as follows:
the values of x, y and z can be found as follows: