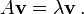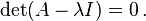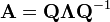The eigenvectors of a square matrix are the non-zero vectors that, after being multiplied by the matrix, remain parallel to the original vector. For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector is scaled when multiplied by the matrix. The prefix eigen- is adopted from the German word "eigen" for "own"[1] in the sense of a characteristic description. The eigenvectors are sometimes also called characteristic vectors. Similarly, the eigenvalues are also known as characteristic values.
The mathematical expression of this idea is as follows:
if A is a square matrix, a non-zero vector v is an eigenvector of A if there is a scalar λ (lambda) such that
The scalar λ (lambda) is said to be the eigenvalue of A corresponding to v. An eigenspace of A is the set of all eigenvectors with the same eigenvalue together with the zero vector. However, the zero vector is not an eigenvector.[2]
These ideas often are extended to more general situations, where scalars are elements of any field, vectors are elements of any vector space, and linear transformations may or may not be represented by matrix multiplication. For example, instead of real numbers, scalars may be complex numbers; instead of arrows, vectors may be functions or frequencies; instead of matrix multiplication, linear transformations may be operators such as the derivative from calculus. These are only a few of countless examples where eigenvectors and eigenvalues are important.
In such cases, the concept of direction loses its ordinary meaning, and is given an abstract definition. Even so, if that abstract direction is unchanged by a given linear transformation, the prefix "eigen" is used, as in eigenfunction, eigenmode, eigenface, eigenstate, and eigenfrequency.
Eigenvalues and eigenvectors have many applications in both pure and applied mathematics. They are used in matrix factorization, in quantum mechanics, and in many other areas.

=============================================================================================================
Characteristic polynomial
The eigenvalues of A are precisely the solutions λ to the equation
============================================================================================================
Eigendecomposition
The spectral theorem for matrices can be stated as follows. Let A be a square n × n matrix. Let q1 ... qk be an eigenvector basis, i.e. an indexed set of k linearly independent eigenvectors, where k is the dimension of the space spanned by the eigenvectors of A. If k = n, then A can be written
where Q is the square n × n matrix whose i-th column is the basis eigenvector qi of A and Λ is the diagonal matrix whose diagonal elements are the corresponding eigenvalues, i.e. Λii = λi.
============================================================================================================
============================================================================================================
Examples in the plane
The following table presents some example transformations in the plane along with their 2×2 matrices, eigenvalues, and eigenvectors.
| horizontal shear | scaling | unequal scaling | counterclockwise rotation by φ | |
| illustration |  |
 |
 | |
| matrix | ||||
| characteristic equation | λ2 − 2λ+1 = (1 − λ)2 = 0 | λ2 − 2λk + k2 = (λ − k)2 = 0 | (λ − k1)(λ − k2) = 0 | λ2 − 2λ cos φ + 1 = 0 |
| eigenvalues λi | λ1=1 | λ1=k | λ1 = k1, λ2 = k2 | λ1,2 = cos φ ± i sin φ = e ± iφ |
| algebraic and geometric multiplicities | n1 = 2, m1 = 1 | n1 = 2, m1 = 2 | n1 = m1 = 1, n2 = m2 = 1 | n1 = m1 = 1, n2 = m2 = 1 |
| eigenvectors |
'Mathematics > Linear Algebra' 카테고리의 다른 글
| LDA (Linear Discriminant Analysis) (4) | 2013.12.21 |
|---|---|
| Cramer’s Formula (0) | 2011.12.21 |
| Matrix Algebra (0) | 2011.12.21 |