Determinant (ex) det(A) , Sarrus, Laplace's formula and the adjugate matrix

336x280(권장), 300x250(권장), 250x250, 200x200 크기의 광고 코드만 넣을 수 있습니다.

determinant

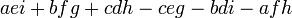$\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}$ is written $\begin{vmatrix} a & b & c\\d & e & f\\g & h & i \end{vmatrix}$ and has the value $aei+bfg+cdh-ceg-bdi-afh\,$ .

Sarrus 방법

http://matrix.skku.ac.kr/sglee/linear/ocu/20301.html

Laplace's formula and the adjugate matrix

Laplace's formula expresses the determinant of a matrix in terms of its minors. The minor M_i,j is defined to be the determinant of the (n−1)×(n−1)-matrix that results from A by removing the i-th row and the j-th column. The expression (−1)^i+jM_i,j is known as cofactor. The determinant of A is given by

$\det(A) = \sum_{j=1}^n (-1)^{i+j} a_{i,j} M_{i,j} = \sum_{i=1}^n (-1)^{i+j} a_{i,j} M_{i,j}.$

Calculating det(A) by means of that formula is referred to as expanding the determinant along a row or column. For the example 3-by-3 matrix $A = \begin{bmatrix}-2&2&-3\\ -1& 1& 3\\ 2 &0 &-1\end{bmatrix}$ , Laplace expansion along the second column (j = 2, the sum runs over i) yields:

$\det(A)\,$	$=\,$	$(-1)^{1+2}\cdot 2 \cdot \det \begin{bmatrix}-1&3\\ 2 &-1\end{bmatrix} + (-1)^{2+2}\cdot 1 \cdot \det \begin{bmatrix}-2&-3\\ 2&-1\end{bmatrix} + (-1)^{3+2}\cdot 0 \cdot \det \begin{bmatrix}-2&-3\\ -1&3\end{bmatrix}$
	$=\,$	$(-2)\cdot((-1)\cdot(-1)-2\cdot3)+1\cdot((-2)\cdot(-1)-2\cdot(-3))$
	$=\,$	$(-2)\cdot(-5)+8 = 18.\,$

저작자표시 비영리 변경금지

'Mathematics > Linear Algebra' 카테고리의 다른 글

adjoint matrix, minor, cofactor (2)	2011.12.21
homogemeous metrix, nonhomogemeous metrix (0)	2011.12.21
inverse metrix, invertible, noninvertible (0)	2011.12.21

Professionality

Determinant (ex) det(A) , Sarrus, Laplace's formula and the adjugate matrix

'Mathematics > Linear Algebra' 카테고리의 다른 글

티스토리툴바

Determinant (ex) det(A) , Sarrus, Laplace's formula and the adjugate matrix

'Mathematics > Linear Algebra' 카테고리의 다른 글

'Mathematics/Linear Algebra' Related Articles

티스토리툴바