336x280(권장), 300x250(권장), 250x250, 200x200 크기의 광고 코드만 넣을 수 있습니다.
determinant
![]() is written
is written  and has the value
and has the value 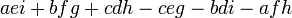 .
.

Sarrus 방법



http://matrix.skku.ac.kr/sglee/linear/ocu/20301.html
Laplace's formula and the adjugate matrix
Laplace's formula expresses the determinant of a matrix in terms of its minors. The minor Mi,j is defined to be the determinant of the (n−1)×(n−1)-matrix that results from A by removing the i-th row and the j-th column. The expression (−1)i+jMi,j is known as cofactor. The determinant of A is given by
Calculating det(A) by means of that formula is referred to as expanding the determinant along a row or column. For the example 3-by-3 matrix  , Laplace expansion along the second column (j = 2, the sum runs over i) yields:
, Laplace expansion along the second column (j = 2, the sum runs over i) yields:
 |
 |
 |
 |
 | |
 |
 |
'Mathematics > Linear Algebra' 카테고리의 다른 글
| adjoint matrix, minor, cofactor (2) | 2011.12.21 |
|---|---|
| homogemeous metrix, nonhomogemeous metrix (0) | 2011.12.21 |
| inverse metrix, invertible, noninvertible (0) | 2011.12.21 |
